Страница 125
1. Объясните, как можно вычислить неизвестное второе слагаемое.
Ответ:
Чтобы вычислить неизвестное второе слагаемое, нужно из суммы вычесть первое слагаемое.
94 + х = 126
х = 126 - 94
х = 32
Проверка: 94 + 32 = 126
2. Какое действие надо выполнить, чтобы найти неизвестное второе слагаемое в каждом из равенств?
408 + а = 1 340 3 360 + х = 25 001
900 + у = 27 000 97 531 + n = 100 050
Сформулируйте правило для нахождения неизвестного второго слагаемого.
Сравните свой ответ с текстом.
Ответ:
Чтобы найти неизвестное второе слагаемое, нужно из суммы вычесть первое слагаемое.
408 + а = 1340
а = 1340 - 408
а = 932
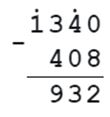
Проверка: 408 + 932 = 1340
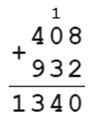
900 + у = 27000
у = 27000 - 900
у = 26100
Проверка: 900 + 26100 = 27000
3360 + х = 25001
х = 25001 - 3360
х = 21641
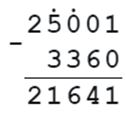
Проверка: 3360 + 21641 = 25001
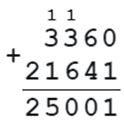
97531 + n = 100050
n = 100050 - 97531
n = 2519
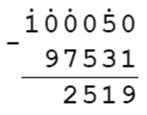
Проверка: 97531 + 2519 = 100050
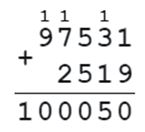
3. Пользуясь правилом, найдите неизвестное второе слагаемое.
12 800 + m = 40 213 893 + k = 2 000
Ответ:
12800 + m = 40213
m = 40213 - 12800
m = 27413
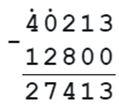
Проверка: 12800 + 27413 = 40213

893 + k = 2000
k = 2000 - 893
k = 1107
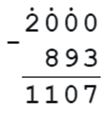
Проверка: 893 + 1107 = 2000

Страница 126
4. Запишите предложение в виде равенства. Найдите неизвестное число.
1) Если к числу 678 прибавить неизвестное число m, то получится 101 200.
2) Если к числу 5 080 прибавить неизвестное число t, то получится 6 117.
Ответ:
1) 678 + m = 101200
m = 101200 - 678
m = 100522
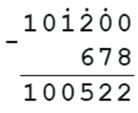
2) 5080 + t = 6117
t = 6117 - 5080
t = 1037
5. Оля задумала число, прибавила его к числу 968 и получила 1 000. Какое число задумала Оля?
Ответ:
х + 968 = 1000
х = 1000 - 968
х = 32
Оля задумала число 32.
6. На базе было 3 450 кг капусты. После того как на базу привезли ещё фургон капусты, там стало 8 700 кг капусты. Сколько капусты привезли на базу?
Ответ:
3450 + х = 8700
х = 8700 - 3450
х = 5250 кг - капусты привезли на базу
7. Объясните, как можно вычислить неизвестный второй множитель.
Ответ:
Чтобы найти неизвестный второй множитель, нужно произведение разделить на первый множитель.
32 • х = 192
х = 192 : 32
х = 6
Проверка: 32 • 6 = 192
8. Какое действие надо выполнить, чтобы найти неизвестный второй множитель в каждом из равенств?
65 • а = 650 506 • b = 2 530
19 • х = 3 800 8 • m = 4 000
Сформулируйте правило для нахождения неизвестного второго множителя.
Сравните свой ответ с текстом.
Ответ:
Чтобы найти неизвестный второй множитель, нужно произведение разделить на первый множитель.
65 • а = 650
а = 650 : 65
а = 10
Проверка: 65 • 10 = 650
19 • х = 3800
х = 3800 : 19
х = 200
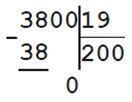
Проверка: 19 • 200 = 3800
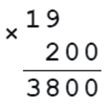
506 • b = 2530
b = 2530 : 506
b = 5
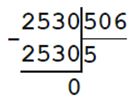
Проверка: 506 • 5 = 2530
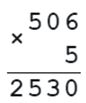
8 • m = 4000
m = 4000 : 8
m = 500
Проверка: 8 • 500 = 4000
Страница 127
9. Запишите предложение в виде равенства.
Найдите неизвестное число.
1) Если 28 умножить на неизвестное число а, то получится 103 432.
2) Если число 312 увеличить в n раз, то получится 4 992.
Ответ:
1) 28 • а = 103432
а = 103432 : 28
а = 3694
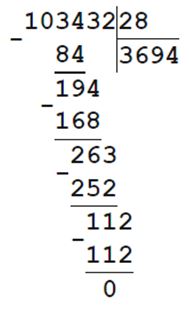
2) 312 • n = 4992
n = 4992 : 312
n = 16
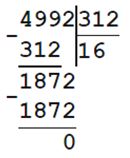
10. Митя задумал число, умножил на него число 960 и получил 336 000. Какое число задумал Митя?
Ответ:
х • 960 = 336000
х = 336000 : 960
х = 350
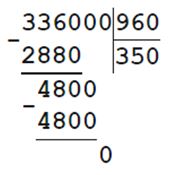
Митя задумал число 350.
11. Объясните, как можно найти неизвестное вычитаемое.
Ответ:
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
198 - х = 39
х = 198 - 39
х = 159
Проверка: 198 - 159 = 39
12. Какое действие надо выполнить, чтобы найти неизвестное вычитаемое в каждом из равенств?
250 - х = 36 500 - n = 144
1 900 - у = 855 4 014 - с = 382
Сформулируйте правило для нахождения неизвестного вычитаемого.
Сравните свой ответ с текстом.
Ответ:
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
250 - х = 36
х = 250 - 36
х = 214
Проверка: 250 - 214 = 36
1900 - у = 855
у = 1900 - 855
у = 1045
Проверка: 1900 - 1045 = 855
500 - n = 144
n = 500 - 144
n = 356
Проверка: 500 - 356 = 144
4014 - с = 382
с = 4014 - 382
с = 3632
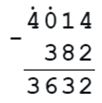
Проверка: 4014 - 3632 = 382
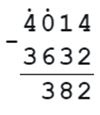
Страница 128
13. Запишите предложение в виде равенства.
Найдите неизвестное число.
1) Если из числа 10 120 вычесть а, то получится 983.
2) Если число 40 308 уменьшить на у, то получится 409.
Ответ:
1) 10120 - а = 983
а = 10120 - 983
а = 9137
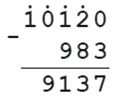
2) 40308 - у = 409
у = 40308 - 409
у = 39899
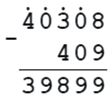
14. Если неизвестное число вычесть из 5 555, то получится 3 939. Чему равно неизвестное число?
Ответ:
х - 5555 = 3939
х = 3939 + 5555
х = 9494 - неизвестное число
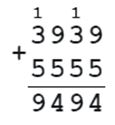
15. У папы было 12 000 р. После покупки пылесоса у него осталось 8 440 р. Какова цена пылесоса?
Ответ:
12000 - х = 8440
х = 12000 - 8440
х = 3560 р. - цена пылесоса
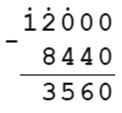
16. На мельнице было 15 450 кг пшеницы. После того как часть пшеницы смололи, осталось 8 600 кг пшеницы.
Сколько пшеницы смололи?
Ответ:
15450 - х = 8600
х = 15450 - 8600
х = 6850 кг - пшеницы - смололи
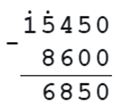
17. Объясните, как можно найти неизвестный делитель.
Ответ:
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
384 : х = 96
х = 384 : 96
х = 4
Проверка: 384 : 4 = 96
Страница 129
18. Какое действие надо выполнить, чтобы найти неизвестный делитель в каждом из равенств?
126 : а = 42 2 700 : с = 900
625 : h = 5 5 400 : х = 54
Сформулируйте правило для нахождения неизвестного делителя.
Сравните свой ответ с текстом.
Ответ:
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
126 : а = 42
а = 126 : 42
а = 3
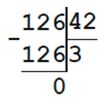
Проверка: 126 : 3 = 42
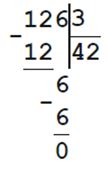
625 : h = 5
h = 625 : 5
h = 125
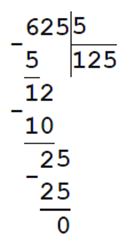
Проверка: 625 : 125 = 5
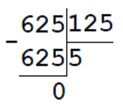
2700 : с = 900
с = 2700 : 900
с = 3
Проверка: 2700 : 3 = 900
5400 : х = 54
х = 5400 : 54
х = 100
Проверка: 5400 : 100 = 54
19. Запишите предложение в виде равенства.
Найдите неизвестное число.
1) Если число 920 разделить на а, то получится 46.
2) Если число 2 100 уменьшить в b раз, то получится 35.
Ответ:
1) 920 : a = 46
а = 920 : 46
а = 20
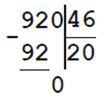
2) 2100 : b = 35
b = 2100 : 35
b = 60
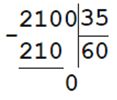
20. На неизвестное число разделили число 14 168 и получили 92. Найдите неизвестное число.
Ответ:
14168 : х = 92
х = 14168 : 92
х = 154 - неизвестное число
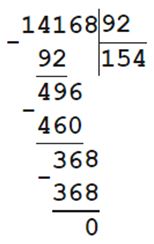
21. Выполните действия.
409 801 - 586 50 308 • 4 830 605 : 5
50 728 + 6 183 320 • 406 17 280 : 36
867 + 995 540 258 • 137 109 296 : 297
Ответ:
22. Вычислите устно.
(100 - 1) • 8 99 • 7 101 • 7
(100 - 2) • 4 98 • 5 101 • 9
(100 - 1) • 6 99 • 9 1 001 • 4
(100 - 2) • 3 97 • 3 1 001 • 5
Ответ:
(100 - 1) • 8 = 792 99 • 7 = 693 101 • 7 = 707
(100 - 2) • 4 = 392 98 • 5 = 490 101 • 9 = 909
(100 - 1) • 6 = 594 99 • 9 = 891 1001 • 4 = 4004
(100 - 2) • 3 = 294 97 • 3 = 291 1001 • 5 = 5005
Страница 130
23. Найдите значения выражений.
64 - 35 + 106 • 402 - 128 : 64
(8 000 - 3 988) • 105 - 945 : 5 • 100
46 839 - (322 060 - 64 - 150) : 20
(753 • 486 - 82 • 105 - 37 048) : 100
(12 460 + 760 • 112) : 41 - 1 791
(34 • 28 - 952) • 161 829 + 5 463 • 60
Ответ:
24. Трое мастеров — Петров, Воробьёв и Зайцев — получили заказ на изготовление 324 матрёшек.
Петров за день может сделать 18 матрёшек, Воробьёв — 20, а Зайцев — 16.
За сколько дней мастера выполнят заказ, если возьмутся за работу одновременно?
Ответ:
1) 18 + 20 + 16 = 54 матрешки - могут сделать трое мастеров за день
2) 324 : 54 = 6 дней - мастера выполнят заказ, если возьмутся за работу одновременно
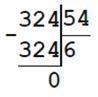
25. Два повара должны испечь 174 пирожка. За час работы один повар может испечь 30 пирожков, а другой — 28.
За сколько часов, работая вместе, они испекут все пирожки?
Ответ:
1) 30 + 28 = 58 пирожков - могут испечь два повара за час работы
2) 174 : 58 = 3 часа - два повара, работая вместе, испекут все пирожки
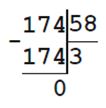
26. Для варки варенья приготовили 45 кг ягод: крыжовник, малину и чёрную смородину.
Крыжовника было 6 кг 500 г, а малины — втрое больше, чем крыжовника.
Сколько чёрной смородины приготовили для варки варенья?
Ответ:
6 кг 500 г = 6500 г
1) 6500 • 3 = 19500 г = 19 кг 500 г - малины приготовили
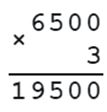
2) 6 кг 500 г + 19 кг 500 г = 26 кг - крыжовника и малины приготовили
3) 45 - 26 = 19 кг - черной смородины приготовили
27. В двух резервуарах было 120 т нефти.
Когда из одного резервуара взяли 35 т 600 кг нефти, а из другого — 46 т 400 кг нефти, в обоих резервуарах нефти осталось поровну. Сколько нефти было в каждом резервуаре первоначально?
Ответ:
1) 35 т 600 кг + 46 т 400 кг = 82 т - нефти - взяли из двух резервуаров
2) 120 - 82 = 38 т - нефти - осталось в двух резервуарах
3) 38 : 2 = 19 т - нефти осталось в каждом резервуаре
4) 35 т 600 кг + 19 т = 54 т 600 кг - нефти было первоначально в первом резервуаре
5) 46 т 400 кг + 19 т = 65 т 400 кг - нефти было первоначально во втором резервуаре
Страница 131
28. В 9 ч утра из города на шоссе выехала машина со скоростью 72 км/ч.
Через полчаса вслед за ней выехал мотоциклист со скоростью 60 км/ч.
На каком расстоянии вдоль шоссе они будут находиться друг от друга в 10 ч утра?
Ответ:
1) 10 - 9 = 1 ч - время, которое проехала машина с 9 ч до 10 ч утра
2) 9 ч + 30 мин = 9 ч 30 мин - выехал из города мотоциклист
3) 10 ч - 9 ч 30 мин = 30 мин - время, которое проехал мотоциклист с 9 ч 30 мин до 10 ч утра
4) 72 • 1 = 72 км - проехала машина за 1 ч
1 ч = 60 мин
60 : 30 = 2, т.е. 30 минут - это половина часа.
5) 60 • 1 : 2 = 30 км - проехал мотоциклист за полчаса
6) 72 - 30 = 42 км - расстоянии между машиной и мотоциклистом в 10 ч утра
29. В упаковке 5 котлет, массой 120 г каждая.
Какова масса четырёх таких упаковок котлет?
Ответ:
1) 120 • 5 = 600 г - масса одной упаковки котлет
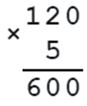
2) 600 • 4 = 2400 г = 2 к 400 г - масса четырех упаковок котлет
30. Выполните действия.
20 ч 16 мин + 1 ч 44 мин
10 ч 25 мин - 9 ч 35 мин
17 ч 30 мин + 2 ч 40 мин
4 мин 57 с + 12 мин 6 с
16 ч 45 мин - 30 мин
27 мин 36 с - 14 мин 42 с
Ответ:
20 ч 16 мин + 1 ч 44 мин = 21 ч 60 мин = 22 ч
10 ч 25 мин - 9 ч 35 мин = 19 ч 60 мин = 20 ч
17 ч 30 мин + 2 ч 40 мин = 19 ч 70 мин = 20 ч 10 мин
4 мин 57 с + 12 мин 6 с = 16 мин 63 с = 17 мин 3 с
16 ч 45 мин - 30 мин = 16 ч 15 мин
27 мин 36 с - 14 мин 42 с = 26 мин 96 с - 14 мин 42 с = 12 мин 54 с
31. Выразите в километрах и метрах: 50 321 м, 8 111 м, 34 780 м, 800 000 м, 123 005 м.
Ответ:
1 км = 1000 м
50321 м = 50 км 321 м
8111 м = 8 км 111 м
34780 м = 34 км 780 м
800000 м = 800 км
123005 м = 123 км 5 м
32. Выразите в метрах: 42 км 120 м, 49 км, 179 км 500 м, 86 км 35 м, 5 км 6 м.
Ответ:
1 км = 1000 м
42 км 120 м = 42120 м
49 км = 49000 м
179 км 500 м = 179500 м
86 км 35 м = 86035 м
5 км 6 м = 5006 м
33. Верно или неверно?
1) При делении числа на 7 в остатке может получиться число 9.
2) Частное 36 000 : 1 800 не изменится, если делимое и делитель разделить на 100.
3) Неверно, что произведение чисел 20 и 30 равно 600.
4) Сумма двух чисел может быть равной одному из слагаемых.
Ответ:
1) При делении числа на 7 в остатке может получиться число 9. - неверно
Остаток должен быть меньше делителя.
2) Частное 36000 : 1800 не изменится, если делимое и делитель разделить на 100. - верно
36000 : 1800 = 20
Если делимое и делитель разделить на 100, то частное не изменится: 360 : 18 = 20
3) Неверно, что произведение чисел 20 и 30 равно 600. - неверно
20 • 30 = 600
4) Сумма двух чисел может быть равной одному из слагаемых. - верно
Если одно из двух слагаемых равно нулю, тогда сумма двух чисел может быть равной одному из слагаемых:
20 + 0 = 20 или 0 + 7 = 0
Страница 132
34. Назовите по два числа, которые при делении на 5 дают в остатке: 2, 3, 4.
Ответ:
17 : 5 = 3 (ост. 2)
32 : 5 = 6 (ост. 2)
28 : 5 = 5 (ост. 3)
43 : 5 = 8 (ост. 3)
39 : 5 = 7 (ост. 4)
54 : 5 = 10 (ост. 4)
35. Какие числа на числовом луче соответствуют отмеченным точкам?
Ответ:
Точка О (0); точка А (20000); точка В (30000); точка С (65000); точка D (80000).
36. На каком участке (А, Б, В, Г, Д, Е) числового луча находятся числа: 267 500, 102 800, 396 125, 184 000, 212 999?
Ответ:
267500 (Г)
102800 (А)
396125 (Е)
184000 (Б)
212999 (В)
37. Учительница показала ученикам модели трёх многогранников.
Дима посмотрел на них сверху и вот что увидел.
Какая из этих фигур является пирамидой; прямоугольным параллелепипедом?
Какая из них может быть кубом? Почему?
Ответ:
38. Оля начертила квадрат. Зоя посмотрела на него и сказала, что это прямоугольник.
Не ошиблась ли Зоя?
Ответ:
Квадрат - это прямоугольник, поэтому Зоя не ошиблась.
Страница 133
39. Какие из высказываний об изображённом угле истинные?
1) ∠AOВ не прямой.
2) ∠АОВ не острый.
3) ∠АОВ острый.
4) ∠АОВ не тупой.
5) ∠АОВ тупой.
6) ∠АОВ острый или прямой.
Ответ:
1) ∠AOВ не прямой.
2) ∠АОВ не острый.
5) ∠АОВ тупой.
40. Определите, в каком из треугольников:
1) есть прямой угол;
2) есть тупой угол;
3) все углы острые;
4) есть не только острый угол, но и прямой;
5) нет прямого угла.
Ответ:
1) есть прямой угол - треугольник 2.
2) есть тупой угол - треугольник 3.
3) все углы острые - треугольник 1.
4) есть не только острый угол, но и прямой - треугольник 2.
5) нет прямого угла - треугольники 1 и 3.
41. Измерьте и сравните длины сторон в каждом из треугольников.
У какого из треугольников:
1) все стороны разной длины;
2) все стороны одной и той же длины;
3) только две стороны имеют одинаковую длину?
Ответ:
1) все стороны разной длины - треугольник 1.
2) все стороны одной и той же длины - треугольник 3.
3) только две стороны имеют одинаковую длину - треугольник 2.
Страница 134
42. Начертите три треугольника со сторонами разной длины так, чтобы в одном треугольнике был прямой угол, в другом — тупой угол, а в третьем — все углы были острыми.
Ответ:
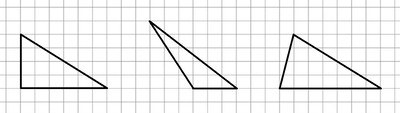
43. В конкурсе детской песни участвовали шестеро четвероклассников — Андреев, Серова, Павлов, Васильев, Белов и Галкина. На диаграмме показано, сколько баллов получил каждый из них.
Кто из участников конкурса получил наибольшее число баллов и кто — наименьшее?
Сколько баллов получила каждая из девочек?
Сколько баллов получил Павлов?
Кто получил больше баллов — Галкина или Васильев — и на сколько?
Ответ:
- Кто из участников конкурса получил наибольшее число баллов и кто - наименьшее?
Наибольшее число баллов (10) - Андреев.
Наименьшее число баллов (3) - Белов.
- Сколько баллов получила каждая из девочек?
Галкина - 4 балла.
Серова - 6 баллов.
- Сколько баллов получил Павлов?
8 баллов.
- Кто получил больше баллов - Галкина или Васильев - и на сколько?
Галкина - 4 балла.
Васильев - 5 баллов.
5 > 4, значит Васильев получил больше баллов.
5 - 4 = 1 балл - Васильев получил больше, чем Галкина
44. Из данных чисел 0, 1, 2, 3, 4, 5, 6, 7, 8 укажите те, которые являются значениями х в неравенствах.
х < 3 х : 2 < 5
х > 4 3 • х > 10
Ответ:
х < 3
При х = 0, 1, 2.
х > 4
При х = 5, 6, 7, 8.
х : 2 < 5
При х = 2, 4, 6, 8.
3 • х > 10
При х = 4, 5, 6, 7, 8.
| Всего комментариев: 0 | |
