Страница 122

1. На складе перед отправкой в магазины пшеничную муку развесили по килограмму в 1 000 пакетов, а ржаную — по килограмму в 100 пакетов. Сколько килограммов муки каждого сорта отправили в магазины?
Ответ:
1) 1 • 1 000 = 1 000 кг - пшеничной муки отправили в магазины
2) 1 • 100 = 100 кг - ржаной муки отправили в магазины

 

2. Верно ли, что 1 т содержит 10 ц?
Ответ:
1 т = 1 000 кг
1 ц = 100 кг
1 т = 1 000 : 100 = 10 ц - верно

 

3. Выразите:
в килограммах: 3 т, 6 т, 14 т, 6 ц, 8 ц, 15 ц;
в центнерах: 5 т, 12 т, 20 т.
Ответ:
3 т = 3 • 1 000 кг = 3 000 кг
6 т = 6 • 1 000 кг = 6 000 кг
14 т = 14 • 1 000 кг = 14000 кг
6 ц = 6 • 100 кг = 600 кг
8 ц = 8 • 100 кг = 800 кг
15 ц = 15 • 100 кг = 1 500 кг

5 т = 5 • 10 ц = 50 ц
12 т = 12 • 10 ц = 120 ц
20 т = 20 • 10 ц = 200 ц

 

4. Во сколько раз 15 т больше 5 ц?
На сколько 15 т больше 5 ц?
На сколько 160 кг меньше 2 ц?
На сколько 4 т больше 4 ц?
На сколько 500 г меньше 4 кг?
Ответ:
1 т = 10 ц 
15 т = 15 • 10 ц = 150 ц
150 : 5 = 30 раз
15 т больше 5 ц в 30 раз

150 - 5 = 145 ц
15 т больше 5 ц на 145 ц

1 ц = 100 кг
2 ц = 2 • 100 кг = 200 кг
200 - 160 = 40 кг
160 кг меньше 2 ц на 40 кг

4 т = 4 • 10 ц = 40 ц
40 - 4 = 36 ц
4 т больше 4 ц на 36 ц

1 кг = 1 000 г
4 кг = 4 • 1 000 г = 4 000 г
4 000 - 500 = 3 500 г
500 г меньше 4 кг на 3 500 г

 

5. На базе было 30 т капусты. На следующий день привезли ещё две трети этого количества. На сколько тонн увеличилась масса капусты на базе?
Ответ:
30 : 3 • 2 = 10 • 2 = 20 т - капусты привезли на следующий день
Следовательно, на 20 т увеличилась масса капусты на базе.

 

Страница 123

6. На двух тракторных прицепах привезли песок, по 5 т на каждом прицепе. Сколько всего килограммов песка привезли?
Ответ:
2 • 5 = 10 т = 10 000 кг - песка привезли всего

 

7. На трёх грузовых машинах привезли картофель, по 3 т на каждой машине. Сколько всего центнеров картофеля привезли?
Ответ:
3 • 3 = 9 т = 90 ц - картофеля привезли всего

 

8. На складе было 4 т сахара. В один магазин отправили 1 265 кг сахара, во второй — на 375 кг больше. Сколько килограммов сахара осталось на складе?
Ответ:

 

9. Составьте задачу и решите её.
Ответ:

 

10. 1) Запишите наибольшее шестизначное число и три следующих за ним при счёте числа.
2) Запишите наименьшее семизначное число и три предшествующих ему при счёте числа.
3) Прочитайте число 1 010 000. Вычтите из него число 1 и запишите результат.
Ответ:
1) 999 999, 1 000 000, 1 000 001.
2) 1 000 000, 999 999, 999 998, 999 997.
3) 1 010 000 - один миллион десять тысяч
1 010 000 - 1 = 1 009 999

 

Страница 124

11. Какие числа нужно записать в пустых клетках таблицы?
Ответ:

 

12. Выполните вычисления.
6 234 - 5 734              10 000 - 3 280 + 40 857
128 060 - 8 179          91 919 + 191 - 7 314
Ответ:

 

13. Найдите значение выражения:
1) х • 42 + у • 107, если х = 14, у = 8;
2) а • m + х, если а = 60, m = 9, х = 360.
Ответ:

 

14. Проверьте равенство, не выполняя вычислений.
64 • 7 + 1 692 = 64 • 8 + 1 692
Ответ:
Равенство неверно, так как в левой части умножают 64 • 7, а в правой 64 • 8, т.е. левая часть будет меньше, чем правая.

 

15. Выполните действия.
96 : 6            52 • 6               350 : 14
88 : 8            248 • 3             (354 - 127) • 100
452 : 3          315 : 9             (398 + 176) • 1000
125 • 8          288 : 60           (1 000 - 408) • 10 000
Ответ:

 

16. Запишите числа в порядке уменьшения: 1 325 337, 13 954 380, 1 522 448, 13 954 270, 1 385 361.
Ответ:
13 954 380, 13 954 270, 1 522 448, 1 385 361, 1 325 337

 

17. Из 3 м ткани получается 2 одинаковых по длине полотенца. Сколько таких полотенец получится из 6 м этой ткани?
Решите задачу двумя способами. Каким способом быстрее получается результат?
Ответ:

 

Страница 125

18. Три швеи сшили по несколько одинаковых наволочек, израсходовав вместе 48 м ткани. Первая швея сшила 6 наволочек, вторая — 10 наволочек, третья — 8 наволочек. Сколько метров ткани израсходовала каждая швея?
Ответ:
1) 6 + 10 + 8 = 24 наволочки - сшили всего
2) 48 : 24 = 2 м - ткани ушло на одну наволочку
3) 6 • 2 = 12 м - ткани израсходовала первая швея
4) 10 • 2 = 20 м - ткани израсходовала вторая швея
5) 8 • 2 = 16 м - ткани израсходовала третья швея

 

19. Назовите координаты центра каждой из окружностей.
Ответ:
Синяя окружность: (4; 4).
Красная окружность: (7; 4).

 

20. По течению реки катер прошёл 150 км за 5 ч. Против течения его скорость была на 12 км/ч меньше, чем по течению. Какое расстояние катер прошёл против течения за 3 ч?
Ответ:
1) 150 : 5 = 30 км/ч - скорость катера по течению
2) 30 - 12 = 18 км/ч - скорость катера против течения
3) 18 • 3 = 54 км - катер прошел против течения за 3 ч

 

21. Изобразите в тетради такие многогранники. Как называется каждый из них?
Ответ:
Первый многогранник - куб.
Второй многогранник - прямоугольный параллелепипед.

 

Страница 126

22. Составьте три задачи, используя данные таблицы, и решите их.
Ответ:

 

23. Рассмотрите многогранник.
Назовите невидимые рёбра: нижней грани; задней грани.
Какие грани видимые и какие невидимые?
Ответ:
Невидимые ребра нижней грани: AB, BC.
Невидимые ребра задней грани: BC, BK.
Видимые грани: AMED, MKOE, DEOC.
Невидимые грани: AMKB, ABCD, BKOC.

 

Марфа купила красных и чёрных ниток. Красных — 2 катушки, а чёрных — на 1 катушку больше. За катушку красных ниток она заплатила 3 р. 50 к., а за катушку чёрных ниток — на 50 к. меньше. Какие нитки обошлись Марфе дороже и на сколько?
Ответ:

 

Страница 127

24. Вычислите площадь четырёхугольника ABCD, если ширина прямоугольника АВСЕ равна 2 см, а длина — 4 см. Известно, что площадь треугольника CED равна 6 см².
Ответ:
1) 4 • 2 = 8 см² - площадь прямоугольника ABCE
2) 8 + 6 = 14 см² - площадь четырехугольника ABCD

 

25. На этикетке товара часто можно увидеть слова «нетто» и «брутто». Нетто — это масса товара без упаковки, а брутто — масса товара с упаковкой. На этикетке банки с огурцами написано: брутто 1 050 г, нетто 900 г. Когда все огурцы съели, мама вымыла банку и положила в неё 650 г томатной пасты. Как теперь должна была бы выглядеть надпись на этикетке?
Ответ:

 

26. За каждое прямое попадание мяча в корзину баскетболисту засчитали 2 очка. При каждом прямом броске Петрова и Васильева мяч попадал в корзину. Судья записал Петрову 24 очка, а Васильеву — 36. На сколько меньше попаданий было у Петрова, чем у Васильева?
Ответ:
1) 24 : 2 = 12 попаданий - было у Петрова
2) 36 : 2 = 18 попаданий - было у Васильева
3) 18 - 12 = 6 попаданий - на столько меньше было у Петрова, чем у Васильева

 

27. Вырежьте из прозрачной или неплотной бумаги два треугольника и наложите их один на другой так, чтобы их общей частью был: 1) пятиугольник; 2) шестиугольник.
Ответ:

 

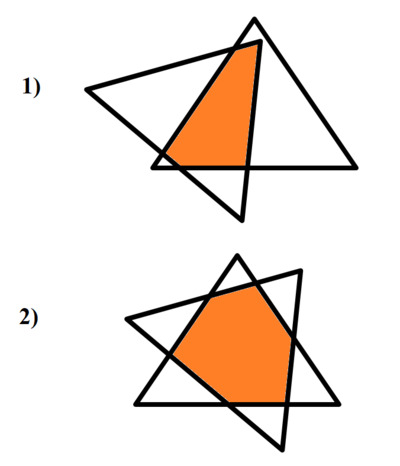
Страница 128

28. Начертите в тетради такой прямоугольник.
Разделите построенный прямоугольник отрезком на два равных прямоугольника. Сколькими способами это можно сделать?
Вычислите периметр каждого прямоугольника. Сколько решений имеет задача?
Ответ:
Прямоугольник можно разделить отрезком на два равных прямоугольника двумя способами.

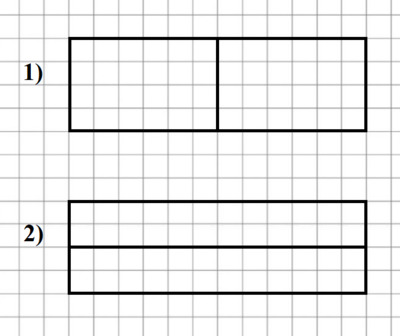
1 способ.
Получатся два прямоугольника со сторонами 3 см и 2 см.
(3 + 2) • 2 = 5 • 2 = 10 см - периметр каждого прямоугольника
2 способ.
Получатся два прямоугольника со сторонами 6 см и 1 см.
(6 + 1) • 2 = 7 • 2 = 14 см - периметр каждого прямоугольника

 

29. В питомник для посадки привезли 480 ягодных кустарников.
На круговой диаграмме показано, какую часть числа всех кустов занимает каждый из видов этих кустарников.
Подсчитайте число кустов смородины, малины, крыжовника и голубики, используя диаграмму.
Ответ:
Кусты смородины - половина всех кустарников.
Кусты малины - четверть всех кустарников.
Кусты крыжовника - восьмая часть всех кустарников.
Кусты голубики - восьмая часть всех кустарников.
480 : 2 = 240 кустов - смородины
480 : 4 = 120 кустов - малины
480 : 8 = 60 кустов - крыжовника
480 : 8 = 60 кустов - голубики

 

30. В кинотеатре на дневной сеанс было продано 300 билетов. Непроданной осталась шестая часть всех билетов. Сколько мест в зале?
Ответ:
1) 300 : 6 = 50 билетов - не продано
2) 300 + 50 = 350 мест - в зале