Страница 40
117. Сколько прямоугольников на рисунке? Запиши длины сторон каждого прямоугольника.
Ответ:
На рисунке изображено 9 прямоугольников: ACEM, ABON, BCDO, NOKM, ODEK, ACDN, NDEM, ABKM, BCEK.
По рисунку видно, что:
AN = BO = CD = 2 см
DE = OK = NM = 3 см
MK = NO = AB = 5 см
AC = ND = ME = 9 см
CE = CD + DE = 2 см + 3 см = 5 см
CE = BK = AM = 5 см
BC = AC - AB = 9 см - 5 см = 4 см
BC = OD = KE = 4 см
Таким образом:
Прямоугольник ACEM: стороны AC и ME = 9 см, стороны CE и AM = 5 см.
Прямоугольник ABON: стороны AB и NO = 5 см, стороны AN и BO = 2 см.
Прямоугольник BCDO: стороны BC и OD = 4 см, стороны CD и BO = 2 см.
Прямоугольник NOKM: стороны NO и MK = 5 см, стороны OK и NM = 3 см.
Прямоугольник ODEK: стороны OD и KE = 4 см, стороны DE и OK = 3 см
Прямоугольник ACDN: стороны AC и ND = 9 см, стороны AN и CD = 2 см
Прямоугольник NDEM: стороны ND и ME = 9 см, стороны DE и NM = 3 см
Прямоугольник ABKM: стороны AB и MK = 5 см, стороны BK и AM = 5 см.
Прямоугольник BCEK: стороны BC и KE = 4 см, стороны CE и BK = 5 см.
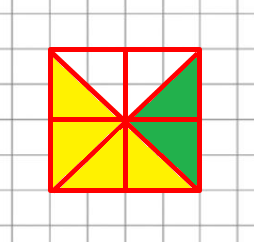
118. 1) Являются ли равнобедренными красные треугольники?
2) Скопируй рисунок, не раскрашивая. Найди и раскрась: равнобедренный треугольник, составленный из двух маленьких, одним цветом; равнобедренный треугольник, составленный из четырёх маленьких, другим цветом.
Ответ:
1) Да, являются, так как у красных треугольников две стороны равны.
2) Зеленым цветом раскрашен равнобедренный треугольник, составленный из двух маленьких треугольников.
Желтым цветом раскрашен равнобедренный треугольник, составленный из четырёх маленьких треугольников.
119. Начерти квадрат со стороной 10 см. Вырежи квадрат и отрежь от него четыре треугольника, как показано на рисунке. Сложи из этих треугольников такой же квадрат, как и оставшийся. Чему равна площадь каждого квадрата?
Ответ:
120. Скопируй рисунок дважды (карандашом). На первом рисунке обведи линии так, чтобы получился параллелепипед, у которого вершина А была бы видимой, а на втором — так, чтобы вершина А была невидимой.
Ответ:
| Всего комментариев: 0 | |
